今天是七夕,看到一则关于“京东”名字来源的八卦,什么东哥的前女友、奶茶妹妹一个排的前男友balabala的,忽然想到能不能用算法对那一个排的前男友聚聚类,看看奶茶妹妹的喜好啊品味啊什么的,然后再看看东哥属于哪一类,一定很有(e)趣(su)。可惜手头没有那一排人的资料,只好作罢。由此看来聚类算法还挺有价值的,比如研究下非诚勿扰、世纪佳缘之类的……
聚类问题
言归正传,所谓聚类问题,就是给定一个元素集合D,其中每个元素具有n个可观察属性,使用某种算法将D划分成k个子集,要求每个子集内部的元素之间相异度尽可能低,而不同子集的元素相异度尽可能高。其中每个子集叫做一个簇(cluster)。
上面这段话翻译为人类语言是这样的:有一堆人,每个人的胸牌上都写着“性别:男/女;年龄:XX”,我们可以根据性别把这堆人分为男、女两个子集,或者根据年龄把他们分为老、中、青、少四个子集。
乍一看,这不还是在做分类操作吗?聚类(clustering)与分类(classification)的不同之处在于:分类是一种示例式的有监督学习算法,它要求必须事先明确知道各个类别的信息,并且断言所有待分类项都有一个类别与之对应,很多时候这个条件是不成立的,尤其是面对海量数据的时候;而聚类是一种观察式的无监督学习算法,在聚类之前可以不知道类别甚至不给定类别数量,由算法通过对样本数据的特征进行观察,然后进行相似度或相异度的分析,从而达到“物以类聚”的目的。
K-Means算法是最简单的一种聚类算法。
K-Means聚类算法
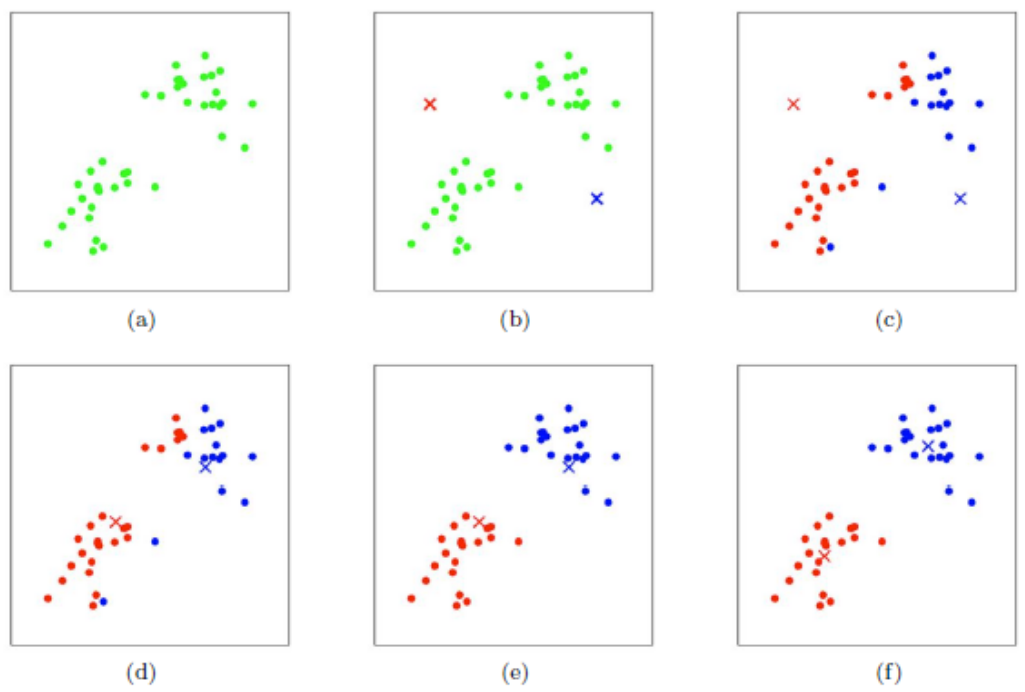
使用K-Means算法进行聚类,过程非常直观:
(a) 给定集合D,有n个样本点
(b) 随机指定两个点,作为两个子集的质心
(c) 根据样本点与两个质心的距离远近,将每个样本点划归最近质心所在的子集
(d) 对两个子集重新计算质心
(e) 根据新的质心,重复操作(c)
(f) 重复操作(d)和(e),直至结果足够收敛或者不再变化
Spark聚类示例
首先还是明确任务,我们要对下面这组数据进行聚类,看看中国足球在亚洲处于什么水平,数据来源于张洋的算法杂货铺。
| 序号 | 国别 | 2006年世界杯 | 2010年世界杯 | 2007年亚洲杯 |
|---|---|---|---|---|
| 1 | 中国 | 50 | 50 | 9 |
| 2 | 日本 | 28 | 9 | 4 |
| 3 | 韩国 | 17 | 15 | 3 |
| 4 | 伊朗 | 25 | 40 | 5 |
| 5 | 沙特 | 28 | 40 | 2 |
| 6 | 伊拉克 | 50 | 50 | 1 |
| 7 | 卡塔尔 | 50 | 40 | 9 |
| 8 | 阿联酋 | 50 | 40 | 9 |
| 9 | 乌兹别克斯坦 | 40 | 40 | 5 |
| 10 | 泰国 | 50 | 50 | 9 |
| 11 | 越南 | 50 | 50 | 5 |
| 12 | 阿曼 | 50 | 50 | 9 |
| 13 | 巴林 | 40 | 40 | 9 |
| 14 | 朝鲜 | 40 | 32 | 17 |
| 15 | 印尼 | 50 | 50 | 9 |
根据数据来源的描述,提前对数据做了如下预处理:对于世界杯,进入决赛圈则取其最终排名,没有进入决赛圈的,打入预选赛十强赛赋予40,预选赛小组未出线的赋予50。对于亚洲杯,前四名取其排名,八强赋予5,十六强赋予9,预选赛没出现的赋予17。这样做是为了使得所有数据变为标量,便于后续聚类。
接下来我们把上面表格中的数据存储在 input/soccer.txt 文件中,属性之间用空格分割:
1 | $ cat input/soccer.txt |
下面是使用Spark来对这组数据进行聚类的Scala代码:
1 | package kmeans |
开发环境与上篇文章相同,不再赘述。接下来把工程导出为jar文件(例如 spark-ml.jar),执行下面的命令:
1 | $ spark-submit --class kmeans.kmeans1 --master local spark-ml.jar |
运行的结果可能是下面这样的:
1 | [40.0,37.33333333333333,10.333333333333332] |
前面三行是 3 个子集的质心,这 3 个子集的索引分别是0、1、2,如果对数据排序,应该是2、0、1。第 4 行 K-Means Cost是各个样本点与质心的距离的平方和,也就是本次聚类的收敛性。后面是 15 个国家的分数及其对应的子集索引,可以看到第一集团(子集2)有日本、韩国、伊朗、沙特,第二集团(子集0)有乌兹别克斯坦、巴林、朝鲜,中国等 8 个国家属于第三集团(好吧,三流就三流吧,还第三集团……)。这个结果与张洋的算法杂货铺中结果相同。
如果多次运行这个程序,下面的结果可能出现的次数最多:
1 | [22.5,12.0,3.5] |
这里的 K-Means Cost 是700,比前面的结果更加收敛。实际应用中也应该多次运行,取收敛性最好的结果(K-Means Cost 最低的)。这次的结果与上次稍有不同,第一集团的伊朗、沙特被归到了第二集团,其他没有变化,无论怎样中国足球总是亚洲三流的。(脚趾头都能想出来,还用Spark来分析,好吧,杀鸡用了牛刀……)
不适用场景
每一种算法都不是放之四海而皆准的,下面是 K-Means 算法不适用的两个场景:
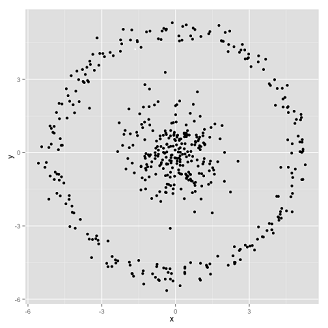
这种情况如果由人来聚类,分分钟搞定,但是 K-Means 算法是这样做的: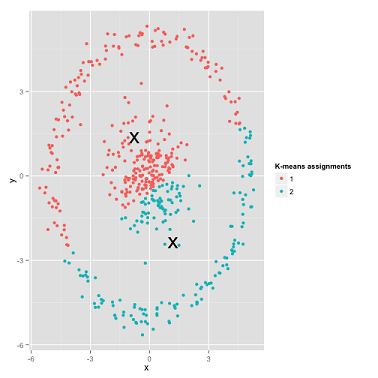
下面这种情况更微妙一些,各个子集的密集程度相差很大: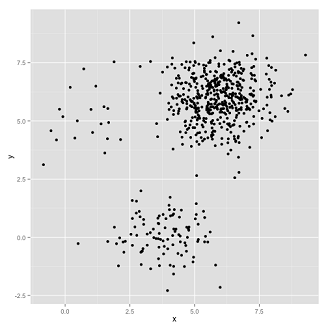
看看 K-Means 算法是怎样做的: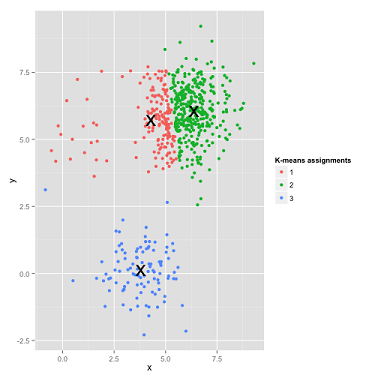
好吧,的确是差成渣了,但这真的不是算法的问题,而是我们人类对算法的选择问题。那么这两种情况应该选择什么算法呢?我现在用尽“洪荒之力”也想不出来,随着学习的深入再来求解吧,或者如果有高人读到这里,请和我联系指点指点吧!